As I have mentioned in my previous blog that an algorithm is said to be correct if it halts and produces correct output for all of its input values.Now in this blog i'm going to explain how to prove an algorithm correct.
To prove correctness of an algorithm, generally we use two most common approach.They are
- Mathematical Induction
- Contradiction
Mathematical Induction can be broadly divided into two category.
- Weak Induction
- Strong Induction
In weak Induction,we commonly use two steps to Prove an algorithm correct.They are
- Base Case or Trivial Case where we claim that the algorithm holds for trivial case(s).
- Inductive step where we prove that the the algorithm is correct for some natural number n+1 or n-1,given that it holds true for n.
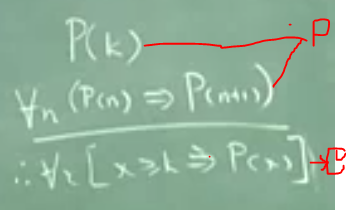P: Premises,C: Conclusion.
The above figure illustrates the definition in terms of Mathematical Logic.The Premises P(K) means the claim is true for trivial case(K could be 0 or any any trivial value), for all (P(n)=>P(n+1)) specifies that if P(n) is true then P(n+1) is also true.If these two Premises are true, Weak Induction concludes that P(x) is true for all x greater than K.
Now we will Prove by weak induction that the sum S(n)=1+3+5+7+.......+2n-1 is equal to square of n for all n>0.
Base case:S(1)=1=1^2 (True),S(2)=1+2(2)-1=1+3=4=2^2 (Holds Good!)
Inductive Step:Let S(k)=k^2; So,1+3+5+7+.......+2k-1=k^2.
Now we can write S(k+1)=1+3+5+.....+(2k-1)+2(k+1)-1
=S(k)+2(k+1)-1[ as S(k)=k^2=1+3+5+7+.......+2k-1]
=k^2+2k+2-1
=k^2+2k+1
=(k+1)^2 (Proved)
Try to prove that a n sided polygon can have almost n(n-3)/2 no of diagonals.
Strong Induction:
In strong induction, to prove P(n) is true, we assume that all k(<n) are true and using all of these we prove that the algorithm is true.
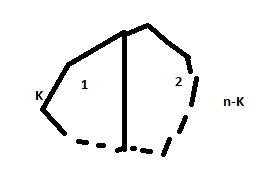
the above figure shows the mathematical definition of Strong Induction.
Now I will use the idea of Strong Induction to prove that sum of interior angle of a n sided polygon is
(n-2)*Pi where Pi=180 degree.
n=3,sum of interior angle is 180 degree=(3-2)*Pi 
n=4,sum of interior angle is 360 degree=(4-2)*Pi
Now,let's assume that the result holds for all k less than n.To Prove the result holds for n sided polygon,1st draw a n sided polygon.
we have divided it into two parts having (K+1) and (n-K+1) no. of edges.Now both (K+1) and (n-K+1) are less than n.So, the sum of interior angle in Polygon 1 is
=(K+1-2)*Pi and sum of interior angle in polygon 2 is
=(n-K+1-2)*Pi.
Hence sum of Interior angle in n sided polygon will be
=(K+1-2)*Pi +(n-K+1-2)*Pi
=(K+1-2+n-K+1-2)*Pi
=(n-2)*Pi .... Proved.
You may go to these link to learn more on strong induction. http://courses.engr.illinois.edu/cs173/sp2009/lectures/lect_18.pdf
**Weak Induction is also called as 1st Principal of Mathematical Induction and Strong Induction is called 2nd Principal of Mathematical Induction
Contradiction
In Proof by Contradiction,we first assume that the statement is false,and next we will show that this assumption implies us that some known and true statement is false.Thus we can conclude that our initial assumption was wrong,i.e the statement is true.
In term of Mathematical Logic,we assume that Statement S is false, i.e not S is true and next we will show that (not S)=>(T and Not T)(where 'and' and 'not' defines logical 'and' and 'or' operation respectively). So,(not S) is false,hence S is true.
Let's see one most common example.
The Theorem says that "There are infinite no of Primes".
Proof: Let The above statement is false, that means that there exists finite number of Primes and let us also assume that all the Prime numbers belong to the set P={p1,p2,.....,pn}.
Now,consider Q=p1*p2*......*pn+1.It's obvious that q is either Prime or Composite.Q is not divisible by any of the Prime Number listed in set P(There remain 1 as remainder).so Q can not be composite.Hence Q is Prime and it does not belong to set P also.So our assumption was wrong.
Hence there exists Infinite number of Primes.
You will get Plenty of examples in Internet.
No comments:
Post a Comment