Introduction:In order to analysis time complexity of an algorithm,we do not go for measuring what amount of time (in ms or second) an algorithm is taking simply because time taken by an algorithm solely depends on the CPU clock speed and Other hardware factors which are not in our(Programmers') control. A CPU having better processing power than another,takes less time to generate output though same code is running in both machine.
Time is in nanoSeconds unit.
Hence it is clear that empirical method is not a reliable yardstick of measuring time complexity of an algorithm.That's why Asymptotic Analysis is used,which doesn't depend on machine or compiler,instead it takes number of steps an algorithm is taking into consideration.
In order to Analysis an algorithm using Asymptotic Notations,we use uniform cost model of computation because of its simplicity.We assign unity cost to compute each mathematical functions(s) (it could be unary or binary arithmetic operation(s), trigonometrical function(s)), initialization, declaration, condition checking, Assignment operations etc.
Now we are in the position of discussing
Asymptotic Upper Bound or Big Oh Notation
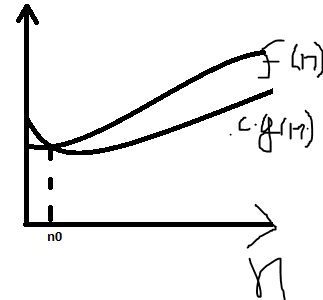
The notation is read as "f of n is big o of g of n". Informally f(n)=O(g(n)) means "f(n) grows not faster than g(n)".Before coming into Mathematical definition,Let's assume f(n) is a real world function( say 100*n^2+3*n+27 or 7*2^(n-1) +5*n^2+47) and g(n) is another function (comparatively simple like n^2 or 2^n).Now,we can say f(n)=O(g(n)) if there exist positive constants c and n(0) such that f(n) <= c*g(n) for all n>=n(0). The following fig. is graphical representation of the definition.
Let's see an example first.
Let (10000+10*n)=f(n)=time taken by n transaction.Consider g(n)=n.Now we will try to find c and n(0) such that f(n)<=c*g(n).If we take c=20,then for all n greater than 1000,g(n) dominates f(n), i.e g(n) is asymptotic upper bound of f(n).Look at the picture below.
Few notes on Big Oh Notation
So,it's clear that total Time taken T=c1+c2+c3=C(say).We call it constant time algorithm( Constant time algorithm refers to those which takes always some constant time regardless of the input size).
It's easy to realize that Total time taken by the algorithm is proportional to the size of Input set.One thing I want to mention that,The complexity of the algorithm is linear not because it takes N no of data as input,but because of traversing the array element.If we are lucky enough,we may get 'X' at the beginning.Then the complexity will be O(1).And in worst case it takes O(N) time.So,For the above code,
Best case running Time =O(1)
Average case running Time =O(N) [O((N+1)/2) =O(N)]
Worst case running Time =O(N).Now you can realize why I have mentioned earlier "Big oh notation doesn't say about what the functions are".
Now I will show the code for Printing all subsets of a given set.A set having N no of elements has 2^n no of subset as power of a set contains 2^n elements.
.
Asymptotic lower bound or Big Omega Notation(Ω)
Big Omega notation defines asymptotic lower bound of an algorithm. Mathematically g(n) is said to be asymptotic lower bound of f(n) if there exist c and n(0) such that for all n >= n(0), f(n)>c*g(n).You may have noticed that It is just reverse of asymptotic upper bound or Big Oh notation.So,we can say f(n) = Ω(g(n)) => g(n)=O(f(n)).So n^2 = Ω (n) as n=O(n^2).
See an example shown below.It will find out whether any two element of an sorted array sums up to X or not. Here I have used Two Pointer Algorithm Design Technique (later we will see more example).
The algorithm is Pretty simple.One may think that running time is proportional to the input size.It's true.But in Best case,We will find the value X by adding 1st and last element(As in linear search,we may get 'x' at the beginning).Hence lower bound of the algorithm is Ω(1).Look at the figure below.
For the given input set,the outer loop run only once.
Asymptotic Tight Bound Or Theta Notation (Θ)
Let f(n) = O(g(n)) and f(n) = Ω(T(n)) (i.e f(n) lies in between c*g(n) and d*T(n) where c and d are constants and n>n(0)).Now if g(n) = T(n) then we can say g(n) is asymptotic tight bound of f(n) i.e f(n) = Θ(g(n)).
Hence f(n) = Θ(g(n)) => f(n) = O(g(n)) and f(n) = Ω(g(n)).
Most important property of Θ notation is that it is symmetric in nature. If n^3 ∈ Θ(3*n^3-7*n+6) then (3*n^3-7*n+6) ∈ Θ(n^3). Similarly, n^3 ∉ Θ(3*n^7-7*n+6) as (3*n^7-7*n+6) ∉ Θ(n^3).
It is not always possible to find tight bound of a function.Ex- f(n) =n(1+sin(n)).
That's end the topic Analysis Of Time complexity.Follow these links to know more.
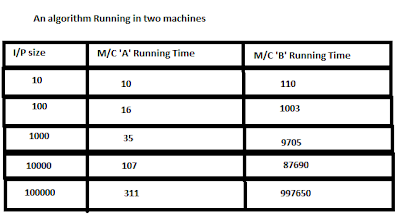 |
| Benchmark Testing |
Time is in nanoSeconds unit.
Hence it is clear that empirical method is not a reliable yardstick of measuring time complexity of an algorithm.That's why Asymptotic Analysis is used,which doesn't depend on machine or compiler,instead it takes number of steps an algorithm is taking into consideration.
In order to Analysis an algorithm using Asymptotic Notations,we use uniform cost model of computation because of its simplicity.We assign unity cost to compute each mathematical functions(s) (it could be unary or binary arithmetic operation(s), trigonometrical function(s)), initialization, declaration, condition checking, Assignment operations etc.
Now we are in the position of discussing
- Asymptotic upper bound or Big Oh Notation.
- Asymptotic lower bound or Big Omega Notation.
- Asymptotic tight bound or Theta notation.
- Small Oh Notation.
- Small Omega Notation.
 |
| Fig-I |
 |
| Ex-1 |
Let (10000+10*n)=f(n)=time taken by n transaction.Consider g(n)=n.Now we will try to find c and n(0) such that f(n)<=c*g(n).If we take c=20,then for all n greater than 1000,g(n) dominates f(n), i.e g(n) is asymptotic upper bound of f(n).Look at the picture below.
 |
| Fig-II |
- One thing we need to remember that, for f(n)=O(g(n)),g(n) is not unique.It refers to the set of functions that satisfy the definition.As f(n) = 10000+10*n
<=10000*n^2+10*n^2 (as n>=0)
<=10010*n^2
=O(n^2) [consider c=10010,n>=0]
Hence g(n)=n^2 is also asymptotic upper bound of the function f(x).Same is true for g(n)= n^3 or g(x)=2^n or g(x)=n!.
- Big Oh doesn't take care about constant terms.There is no difference between O(2*n) and O(n).But O(e^(2*n)) != O(e^n) or O(5^n) != O(2^n) because one term is not constant factor of another.
- Big oh notation doesn't say about what the functions are.Later I'll explain this topic.
Now,Let's try to calculate upper bound of an algorithm with the help of few basic code.Codes written here are all in C++.If you don't know C++ very well,follow http://www.cplusplus.com/reference/ .It is really helpful.Also you can follow "Thinking In C++" by Bruce Eckel.
- First try to understand the code having constant time complexity.
 |
| Source Code 1 |
- Let's see an example of Linear Time Algorithm.
It's easy to realize that Total time taken by the algorithm is proportional to the size of Input set.One thing I want to mention that,The complexity of the algorithm is linear not because it takes N no of data as input,but because of traversing the array element.If we are lucky enough,we may get 'X' at the beginning.Then the complexity will be O(1).And in worst case it takes O(N) time.So,For the above code,
Best case running Time =O(1)
Average case running Time =O(N) [O((N+1)/2) =O(N)]
Worst case running Time =O(N).Now you can realize why I have mentioned earlier "Big oh notation doesn't say about what the functions are".
 |
| Source Code 3 |
The outer loop iterates 2^n number of times and for each value of 'i', 'j' runs at least once and 'k'runs exactly n times in inner loop.So,roughly(avoiding complex terms and taking a bit simple and dominating) the complexity of above algorithm is O(n*2^n).One most important thing about the above algorithm is that performance of these kind of code partly depends on output.That's why they are also called Output Sensitive algorithm.Here printing 2^n number contributes significantly to the running time of the code.That's end our discussion on Big Oh notation.Now I will explain Big Omega Notation
.
Asymptotic lower bound or Big Omega Notation(Ω)
Big Omega notation defines asymptotic lower bound of an algorithm. Mathematically g(n) is said to be asymptotic lower bound of f(n) if there exist c and n(0) such that for all n >= n(0), f(n)>c*g(n).You may have noticed that It is just reverse of asymptotic upper bound or Big Oh notation.So,we can say f(n) = Ω(g(n)) => g(n)=O(f(n)).So n^2 = Ω (n) as n=O(n^2).
See an example shown below.It will find out whether any two element of an sorted array sums up to X or not. Here I have used Two Pointer Algorithm Design Technique (later we will see more example).
 |
| Source Code 4 |
 |
Asymptotic Tight Bound Or Theta Notation (Θ)
Let f(n) = O(g(n)) and f(n) = Ω(T(n)) (i.e f(n) lies in between c*g(n) and d*T(n) where c and d are constants and n>n(0)).Now if g(n) = T(n) then we can say g(n) is asymptotic tight bound of f(n) i.e f(n) = Θ(g(n)).
Hence f(n) = Θ(g(n)) => f(n) = O(g(n)) and f(n) = Ω(g(n)).
 |
| Fig 2 |
It is not always possible to find tight bound of a function.Ex- f(n) =n(1+sin(n)).
That's end the topic Analysis Of Time complexity.Follow these links to know more.
- 1.http://www.youtube.com/watch?v=ca3e7UVmeUc
- http://www.youtube.com/watch?v=VIS4YDpuP98
- http://www.youtube.com/watch?v=NfRp1Yhw8EQ
- https://en.wikipedia.org/wiki/Big_O_notation
- http://en.wikipedia.org/wiki/Analysis_of_algorithms

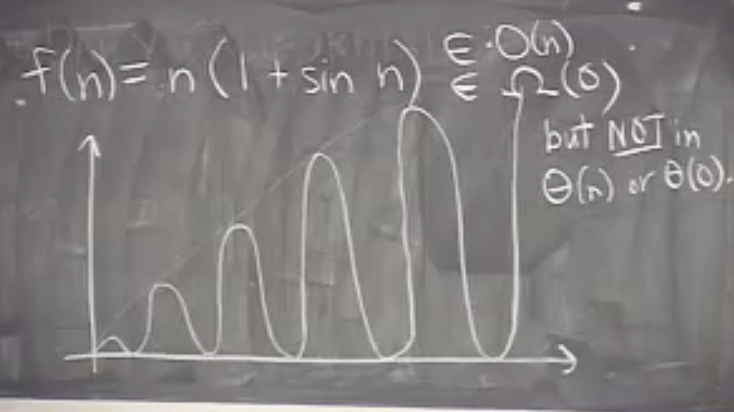
No comments:
Post a Comment