Analysis of Time Complexity

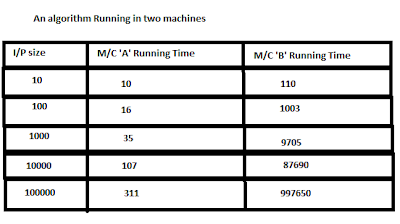
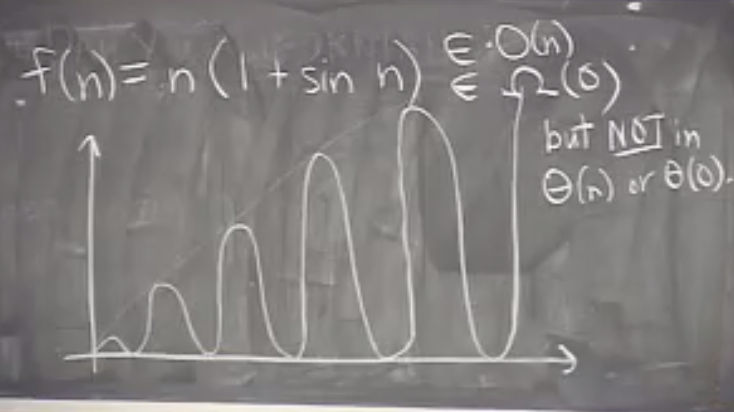Introduction:In order to analysis time complexity of an algorithm,we do not go for measuring what amount of time (in ms or second) an algorithm is taking simply because time taken by an algorithm solely depends on the CPU clock speed and Other hardware factors which are not in our(Programmers') control. A CPU having better processing power than another,takes less time to generate output though same code is running in both machine.

Benchmark Testing

Time is in nanoSeconds unit.












Hence it is clear that empirical method is not a reliable yardstick of measuring time complexity of an algorithm.That's why Asymptotic Analysis is used,which doesn't depend on machine or compiler,instead it takes number of steps an algorithm is taking into consideration.
In order to Analysis an algorithm using Asymptotic Notations,we use uniform cost model of computation because of its simplicity.We assign unity cost to compute each mathematical functions(s) (it could be unary or binary arithmetic operation(s), trigonometrical function(s)), initialization, declaration, condition checking, Assignment operations etc.
Now we are in the position of discussing

• Asymptotic upper bound or Big Oh Notation.
• Asymptotic lower bound or Big Omega Notation.
• Asymptotic tight bound or Theta notation.

There are other two notations,but I will not discuss them because they are less use in compare to above three notation.They are

• Small Oh Notation.
• Small  Omega Notation.

                  Asymptotic Upper Bound or Big Oh Notation

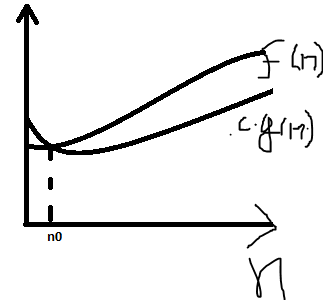
The notation is read as "f of n is big o of g of n". Informally f(n)=O(g(n)) means "f(n) grows not faster than g(n)".Before coming into Mathematical definition,Let's assume f(n) is a real world function( say 100*n^2+3*n+27 or 7*2^(n-1) +5*n^2+47)  and  g(n) is another function (comparatively simple like n^2 or 2^n).Now,we can say f(n)=O(g(n)) if there exist positive constants c and n(0) such that f(n) <= c*g(n) for all n>=n(0). The following fig. is graphical representation of  the definition.

Fig-I

Let's see an example first.

Ex-1

Let (10000+10*n)=f(n)=time taken by n transaction.Consider g(n)=n.Now we will try to find c and n(0) such that f(n)<=c*g(n).If we take c=20,then for all n greater than 1000,g(n) dominates f(n), i.e g(n) is asymptotic upper bound of f(n).Look at the picture below.

Fig-II
      

                        Few notes on Big Oh Notation

• One thing we need to remember that, for f(n)=O(g(n)),g(n) is not unique.It refers to the set of functions that satisfy the definition.As f(n) = 10000+10*n

       <=10000*n^2+10*n^2 (as n>=0)

       <=10010*n^2

        =O(n^2) [consider c=10010,n>=0]

       Hence g(n)=n^2 is also asymptotic upper bound of the function f(x).Same is true for g(n)= n^3 or g(x)=2^n or g(x)=n!.

• Big Oh doesn't take care about constant terms.There is no difference between O(2*n) and O(n).But O(e^(2*n)) != O(e^n) or  O(5^n) !=  O(2^n) because one term is not constant factor of another.
• Big oh notation doesn't say about what the functions are.Later I'll explain this topic.

                              Calculation of Upper Bound 

Now,Let's try to calculate upper bound of an algorithm with the help of few basic code.Codes written here are all in C++.If you don't know C++ very well,follow http://www.cplusplus.com/reference/ .It is really helpful.Also you can follow "Thinking In C++" by Bruce Eckel.

•  First try to understand the code having constant time complexity.

 Source Code 1

So,it's clear that total Time taken  T=c1+c2+c3=C(say).We call it constant time algorithm( Constant time algorithm refers to those which takes always some constant time regardless of the input size).

• Let's see  an example of Linear Time Algorithm.

It's easy to realize that Total time taken by the algorithm is proportional to the size of Input set.One thing I want to mention that,The complexity of the algorithm is linear not because it takes N no of data as input,but because of traversing the array element.If we are lucky enough,we may get  'X' at the beginning.Then the complexity will be O(1).And in worst case it takes O(N) time.So,For the above code,
Best case running Time =O(1)
Average case running Time =O(N) [O((N+1)/2) =O(N)]
Worst case running Time =O(N).Now you can realize why I have mentioned earlier "Big oh notation doesn't say about what the functions are".

Now I will show the code for Printing all subsets of a given set.A set having N no of elements has 2^n no of subset as power of a set contains 2^n elements.

Source Code 3

The outer loop iterates 2^n number of times and for each value of  'i', 'j' runs at least once and 'k'runs exactly n times in inner loop.So,roughly(avoiding complex terms and taking a bit simple and dominating) the complexity of above algorithm is O(n*2^n).One most important thing about the above algorithm is that performance of these kind of code partly depends on output.That's why they are also called Output Sensitive algorithm.Here printing 2^n number contributes significantly to the running time of the code.

That's end our discussion on Big Oh notation.Now I will explain Big Omega Notation
.
         Asymptotic lower bound or Big Omega Notation(Ω)
Big Omega notation defines asymptotic lower bound of an algorithm. Mathematically g(n) is said to be asymptotic lower bound of f(n) if there exist c and n(0) such that for all n >= n(0), f(n)>c*g(n).You may have noticed that It is just reverse of asymptotic upper bound or Big Oh notation.So,we can say f(n) = Ω(g(n)) => g(n)=O(f(n)).So n^2 = Ω (n) as n=O(n^2).

See an example shown below.It will find out whether any two element of an sorted array sums up to X or not. Here I have used Two Pointer Algorithm Design Technique (later we will see more example).

Source Code 4

The algorithm is Pretty simple.One may think that running time is proportional to the input size.It's true.But in Best case,We will find the value X by adding 1st and last element(As in linear search,we may get 'x' at the beginning).Hence lower bound of the algorithm is Ω(1).Look at the figure below.

For the given input set,the outer loop run only once.








        
            Asymptotic Tight Bound Or Theta Notation (Θ)
Let f(n) = O(g(n)) and f(n) = Ω(T(n)) (i.e f(n) lies in between c*g(n) and d*T(n) where c and d are constants and n>n(0)).Now if g(n) = T(n) then we can say g(n) is asymptotic tight bound of f(n) i.e f(n) = Θ(g(n)).
Hence  f(n) = Θ(g(n))  =>  f(n) = O(g(n)) and f(n) = Ω(g(n)).

Fig 2

Most important property of Θ notation is that it is symmetric in nature. If n^3 ∈ Θ(3*n^3-7*n+6)  then (3*n^3-7*n+6)  ∈ Θ(n^3). Similarly, n^3 ∉ Θ(3*n^7-7*n+6) as (3*n^7-7*n+6) ∉ Θ(n^3).
It is not always possible to find tight bound of a function.Ex- f(n) =n(1+sin(n)).

That's end the topic Analysis Of Time complexity.Follow these links to know more.

1. 1.http://www.youtube.com/watch?v=ca3e7UVmeUc
2. http://www.youtube.com/watch?v=VIS4YDpuP98
3. http://www.youtube.com/watch?v=NfRp1Yhw8EQ
4. https://en.wikipedia.org/wiki/Big_O_notation
5. http://en.wikipedia.org/wiki/Analysis_of_algorithms

Correctness Proving Methods

As I have mentioned in my previous blog that an algorithm is said to be correct if it halts and produces correct output for all of its input values.Now in this blog i'm going to explain how to prove an algorithm correct.

To prove correctness of an algorithm, generally we use two most common approach.They are

1. Mathematical Induction
2. Contradiction 

                   Mathematical Induction

Mathematical Induction can be broadly divided into two category.

1. Weak Induction
2. Strong Induction

Weak Induction:

In weak Induction,we commonly use two steps to Prove an algorithm correct.They are

• Base Case or Trivial Case where we claim that the algorithm holds for trivial case(s).
• Inductive step where we prove that the the algorithm is correct for some natural number n+1 or n-1,given that it holds true for n.

P: Premises,C: Conclusion.

The above figure illustrates the definition in terms of Mathematical Logic.The Premises P(K) means the claim is true for trivial case(K could be 0 or any any trivial value), for all (P(n)=>P(n+1)) specifies that if P(n) is true then P(n+1) is also true.If these two Premises are true, Weak Induction concludes that P(x) is true for all x greater than K.

Now we will Prove by weak induction that the sum S(n)=1+3+5+7+.......+2n-1 is equal to square of n for all n>0.

Base case:S(1)=1=1^2 (True),S(2)=1+2(2)-1=1+3=4=2^2 (Holds Good!)

Inductive Step:Let S(k)=k^2; So,1+3+5+7+.......+2k-1=k^2.

Now we can write S(k+1)=1+3+5+.....+(2k-1)+2(k+1)-1

                                        =S(k)+2(k+1)-1[ as S(k)=k^2=1+3+5+7+.......+2k-1]

                                        =k^2+2k+2-1

                                        =k^2+2k+1

                                        =(k+1)^2 (Proved)

Try to prove that a n sided polygon can have almost n(n-3)/2 no of diagonals.

Strong Induction:

In strong induction, to prove P(n) is true, we assume that all k(<n) are true and using all of these we prove that the algorithm is true.

the above figure shows the mathematical definition of Strong Induction.

Now I will use the idea of Strong Induction to prove that sum of interior angle of a n sided polygon is 

(n-2)*Pi where Pi=180 degree.

                         

n=3,sum of interior angle is 180 degree=(3-2)*Pi            

n=4,sum of interior angle is 360 degree=(4-2)*Pi 

Now,let's assume that the result holds for all k less than n.To Prove the result holds for n sided polygon,1st draw a n sided polygon.

we have divided it into two parts having (K+1) and (n-K+1) no. of  edges.Now both (K+1) and (n-K+1) are less than n.So, the sum of interior angle in Polygon 1 is

=(K+1-2)*Pi and sum of interior angle in polygon 2 is

=(n-K+1-2)*Pi.

Hence sum of Interior angle in n sided polygon will be

=(K+1-2)*Pi +(n-K+1-2)*Pi

=(K+1-2+n-K+1-2)*Pi

=(n-2)*Pi .... Proved.

You may go to these link to learn more on strong induction. http://courses.engr.illinois.edu/cs173/sp2009/lectures/lect_18.pdf

https://www.google.co.in/url?sa=t&rct=j&q=&esrc=s&source=web&cd=4&cad=rja&ved=0CEEQFjAD&url=http%3A%2F%2Fwww.ohio.edu%2Fpeople%2Fmelkonia%2Fmath306%2Fslides%2Finduction4.ppt&ei=OE6_Ufr3CI7yrQelqoGIBA&usg=AFQjCNHIhGxraJ_xkfH5a7qEVk7wA62jfA&sig2=3KpBevPto3n5Dmfe9t8E9w&bvm=bv.47883778,d.bmk

**Weak Induction is also called as 1st Principal of Mathematical Induction and Strong Induction is called 2nd Principal of Mathematical Induction

   

                                              Contradiction

In Proof by Contradiction,we first assume that the statement is false,and next we will show that this assumption implies us that some known and true statement is false.Thus we can conclude that our initial assumption was wrong,i.e the statement is true.

In term of Mathematical Logic,we assume that Statement S is false, i.e not S is true and next we will show that (not S)=>(T and Not T)(where 'and' and 'not' defines logical 'and' and 'or' operation respectively). So,(not S) is false,hence S is true.

Let's see one most common example.

The Theorem says that "There are infinite no of Primes". 

Proof: Let The above statement is false, that means that there exists finite number of Primes and let us also assume that all the Prime numbers belong to the set  P={p1,p2,.....,pn}.

Now,consider Q=p1*p2*......*pn+1.It's obvious that q is either Prime or Composite.Q is not divisible by any of the Prime Number listed in set P(There remain 1 as remainder).so Q can not be composite.Hence Q is Prime and it does not belong to set P also.So our assumption was wrong.

Hence there exists Infinite number of Primes.

You will get Plenty of examples in Internet.

Introduction To Algorithm

                        What Is Algorithm?
Before defining algorithm , Let's consider a function y=f(x).What does it mean actually?Here f is nothing but a machine which takes a value of  x as raw material and produces y as product depending on raw material (i.e x).For example ,f(x)=x^2(consider x belongs to set of integer),it is a function (or machine) that gives the square of a integer as output which is given as input to the function.
In Computer Science (and in Mathematics also), algorithm is a set of instructions (or collection of procedures you can say) which takes some value(s) as  input and after step by step processing the value(s) (as specified by the set of instructions) it produces output in some finite time.It can be written in English,Computer Program or even as a Hardware design.

                               Why Do We Learn Algorithm?
No doubt,Design and Analysis of Algorithm is the most challenging and interesting area of computer science.It helps to think a problem more mathematically as well as abstractly.To become a Class creator or Application Programmer in a company one should have a good knowledge on this subject.Algorithm is required in almost all fields of Computer Science.consider Theoretical Computer Science,you need K.M.P string matching algorithm,in Computer Networks you need Routing Algorithms(Static and Dynamic), in Cryptography and Security you use R.S.A Algorithm etc.

           Characteristics Of A Good Algorithm

•  Finiteness : The most basic and necessary characteristics of an Algorithm is Finiteness. It must terminate after a finite no of steps and each step must be executable in finite amount of time. An algorithm is said to be incorrect if it does not halt for any of its input value.
• Effectiveness : Each step of a good algorithm Should be effective.It must have some significance related to the solution of the problem(i.e it contribute something to reach the closer to the actual solution).Otherwise it unnecessarily increases time and memory overhead.
• besides a good algorithm should be Unambiguous,Divided into Modules and Easy to Understand.